Introduction

This is the new C++ implementation of UESMANN, based on the original code used in my thesis. That code was written as a .angso library for the Angort language, and has evolved to become rather unwieldly (as well as being intended for use from a language no-one but me uses).

The code is very simplistic, using scalar as opposed to matrix operations and no GPU acceleration. This is to make the code as clear as possible, as befits a reference implementation, and also to match the implementation used in the thesis. There are no dependencies on any libraries beyond those found in a standard C++ install, and libboost-test for testing. You may find the code somewhat lacking in modern C++ style because I'm an 80's coder.

I originally intended to write use Keras/Tensorflow, but would have been limited to using the low-level Tensorflow operations because of the somewhat peculiar nature of optimisation in UESMANN: we descend the gradient relative to the weights for one function, and the gradient relative to the weights times some constant for the other. A Keras/Tensorflow implementation is planned.

Implementations of the other network types mentioned in the thesis are also included.

The top level class is Net, which is an virtual type describing the neural net interface and performing some basic operations. Other classes are:

NetFactory, which creates, loads and saves these concrete subclasses of Net:
- BPNet, a plain, unmodulated MLP trained with backprop
- OutputBlendingNet and HInputNet, which are alternative modulatory networks described below
- UESNet, the UESMANN network
ExampleSet, which is a set of examples for training networks
Net::SGDParams, which controls how training is performed (including crossvalidation and hyperparameters)
MNIST, which encapsulates MNIST-format data sets and from which ExampleSet instances can be generated.

The library and test executables

The entire library is include-only, just include netFactory.hpp to get everything. The provided CMakeLists.txt builds two executables:

uesmann-test runs a set of test suites written using the Boost test framework.
genBoolGrid trains 1000 UESMANN networks for every possible binary boolean function pairing and calculates how many perform the required function (this test was designed to ensure that the library's output matched that from equivalent code used in the thesis).

The network

The network implemented is a modified version of the basic Rumelhart, Hinton and Williams multilayer perceptron with a logistic sigmoid activation function, and is trained using stochastic gradient descent by the back-propagation of errors. The modification consists of a modulatory factor 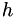$h$ , which essentially doubles all the weights at 1, while leaving them at their nominal values at 0. Each node has the following function:

$y = \sigma\left(b+(h+1)\sum_i w_i x_i\right),$

where

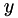is the node output,
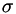$\sigma$ is the "standard" logistic sigmoid activation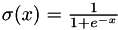 $\sigma(x) = \frac{1}{1+e^{-x}}$
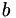is the node bias,
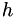is the modulator,
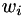are the node weights,
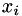are the node inputs.

The network is trained to perform different functions at different modulator levels, currently two different functions at h=0 and h=1. This is done by modifying the back-propagation equations to find the gradient 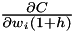$\frac{\partial C}{\partial w_i(1+h) }$ (i.e. the cost gradient with respect to the modulated weight). Each example is tagged with the appropriate modulator value, and the network is trained by presenting examples for alternating modulator levels so that the mean gradient followed will find a compromise between the solutions at the two levels.

It works surprisingly well, and shows interesting transition behaviour as the modulator changes. In the thesis, it has been tested on:

boolean functions: all possible pairings of binary boolean functions can be performed in the same parameter space as a single boolean function (i.e. two hidden nodes);
image classification: it performs well on line recognition tasks, modulating between horizontal and vertical line recognition in noisy images; and on the MNIST handwriting recognition task, modulating between recognising digits with their nominal labelling and an alternate labelling with a maximal Hamming distance;
robot control: in a homeostatic robot task, a real robot transitioned between exploration and phototaxis as simulated battery charge (which provided the modulator) fell.

The performance of UESMANN was tested against:

output blending: performing modulation by training two networks, one for each modulation level, and interpolating between the outputs using the modulator
h-as-input: providing the the modulator h as as extra input to a plain MLP and training accordingly.

No enhancements of any kind were used in either UESMANN or the other networks to provide a baseline performance with no confounding factors. This means no regularisation, no adaptive learning rate, not even momentum (Nesterov or otherwise).

Examples

The files named test.. have various unit tests in them which can be useful examples. The Tests page shows some of these tests in more detail.